Operaciones y conversiones con numeros binarios, octales y hexadecimales

Nidia Muñoz

CONVERSIONES

 DE DECIMAL A BINARIO

Lo primero que vamos a hacer es convertir el número 77₁₀ en su equivalente binario, lo cual también nos va a facilitar su conversión a octal y hexadecimal.

Para realizar dicha conversión, primero vamos a dividir el número 77 entre 2 que es la base del sistema binario y luego sus cocientes también entre 2 tantas veces sea posible hasta que el cociente sea 1, así:

Cuando ya tengamos las divisiones, tomamos el último cociente y los residuos de derecha a izquierda y de abajo hacia arriba como se muestra en la imagen. Al ordenarlos obtendremos el equivalente de 77₁₀ en binarios:  1001101₂

DE BINARIO A OCTAL

Como ya tenemos el número 77₁₀ convertido en el número binario correspondiente que es 1001101₂, con ayuda de la tabla de octales lo pasamos a convertimos dividiéndolo en cantidades de 3 cifras de izquierda a derecha y buscando su equivalente en el sistema octal así:

Para obtener el número equivalente el octal, tomamos los números que sacamos de la tabla de izquierda a derecha y obtenemos que 77₁₀ en octal es igual a 115_8.

DE BINARIO A HEXADECIMAL

Esta manera es similar a la anterior. Ya tenemos el número 77₁₀ convertido en el número binario correspondiente que es 1001101₂ entonces, con ayuda de la tabla de hexadecimales lo convertimos dividiéndolo en cantidades de 4 cifras de izquierda a derecha y buscando su equivalente en el sistema hexadecimal así:

 

Para obtener el número equivalente el hexadecimal, tomamos las cifras que obtenemos de la tabla de izquierda a derecha y obtenemos que 77₁₀ en hexadecimal es igual a 4D_16.

OPERACIONES

    Como ejemplo vamos a sumar, restar, multiplicar y dividir los dos primeros y los dos últimos   dígitos de nuestra cédula.

    Para esto lo primero que vamos a hacer es convertir los números que se encuentran expresados en números decimales a números binarios. Para realizar dicha conversión, primero vamos a dividir el número  entre 2 que es la base del sistema binario y luego sus cocientes también entre 2 tantas veces sea         posible hasta que el cociente sea 1. En mi caso quedaran así:

Cuando ya tengamos las divisiones, tomamos el último cociente y los residuos de derecha a izquierda y de abajo hacia arriba como se muestra en la imagen. Al ordenarlos obtendremos el equivalente en binarios.     10₁₀ = 1010   y   77₁₀ = 1001101

SUMA DE BINARIOS

Para sumar números binarios debemos hacerlo como en el sistema decimal. Iniciamos sumando desde la derecha y terminamos en el último par de números de la izquierda, esto teniendo en cuenta las reglas para sumar números binarios que están en la tabla:

Como se puede observar, la suma se efectuó iniciando de los valores de la derecha que son 1 + 0 los cuales dan como resultado 1 según la tabla. Esto se hace con todos los demás números. En el caso de 1 + 1 el cual nos da como resultado 10, se deja el 0 y se lleva 1 en la siguiente cifra y se lo suma junto con los dígitos correspondientes. Las que quedan sueltas se bajan sin operar.

RESTA DE BINARIOS

La resta binaria es similar a la resta decimal. Al igual que en la decimal vamos a realizarla de derecha a izquierda. Vamos a restar teniendo en cuenta la tabla de reglas de la resta binaria de la siguiente manera:

Como se puede observar, la suma se efectuó iniciando de los valores de la derecha que son 1 - 0 los cuales dan como resultado 1 según la tabla. Esto se hace con todos los demás números. En el caso de 0 - 1 el cual nos da como resultado 11, se deja un 1 y se lleva el otro 1 en la siguiente cifra. Este dígito que llevamos qué es el 1 debe ser restado de la cifra que está en el minuendo al que se la lleva, aquí en este caso la cifra es 1 así que quedara 1 - 1 = 0 y el resultado qué es 0 se opera con el sustraendo que es 0 para lo cual nos dará 0 - 0 = 0 el cual se tomará como cifra final y se colocara en el resultado. Las que quedan sueltas se bajan sin operar.

MULTIPLICACIÓN DE BINARIOS

Para multiplicar números binarios debemos hacerlo como en el sistema decimal. Iniciamos multiplicando desde la derecha y terminamos en el último par de números de la izquierda, se multiplica cada número de la parte inferior por todos los factores de la parte superior teniendo en cuenta las reglas para multiplicar números binarios que están en la tabla y al final se hace una suma binaria de los productos obtenidos para obtener el resultado final.

Como se puede observar, la multiplicación se efectuó iniciando con los valores de la derecha que son 1 x 0 los cuales dan como resultado 0 según la tabla. Esto se hace con todos los demás números. Al ubicar los productos que se obtienen de multiplicar cada número por los demás se debe correr una cifra hacia la izquierda como se ve en el ejemplo. Al final se realiza la sumatoria de los productos.

DIVISIÓN DE BINARIOS

Para dividir a los binarios se hace un proceso similar al que se hace para dividir números decimales. Para dividir es necesario saber diferenciar qué un número es mayor a otro en los binarios. Primero se debe ver cuántas cifras hay en el divisor y tomar el mismo número en el dividendo, si el número que queda en el dividendo es menor al número del divisor se debe tomar una cifra más en el dividendo.

Ya habiendo cumplido con los criterios en la comparación se agrega 1 al cociente y debajo de las cifras tomadas en el dividendo, se ubica el número que está en el divisor de derecha a izquierda y se procede a realizar una resta binaria entre estos números. En nuestro ejemplo sería 10011 - 1010 = 1001 y a esta diferencia se procede a agregar o bajar el siguiente número del dividendo que quedó sin tomar, en nuestro ejemplo es 0 y queda 10010. Si el número que se bajó no es suficiente para que la cifra de la diferencia sea mayor al divisor, se coloca 0 en el cociente y se procede a bajar la siguiente cifra. Luego de esto se vuelve a restar el divisor del número que nos quedó y esto se repite sucesivamente hasta que ya no queden cifras por bajar al igual que en la división decimal.

---

Simón Rodríguez

CONVERSIONES

Ultimos dos digitos de la cedula: 86

 DE DECIMAL A BINARIO

Para convertir un número decimal a binario, hay que divdir el número entre 2 tantas veces como se pueda, posteriormente se unen el cociente de la ultima division y los residuos de las todas las divisiones de derecha a izquierda. Utilizando este procedimiento con el numero 86, podemos ver que su equivalente en base 2 es:  1010110 ₂

DE DECIMAL A OCTAL

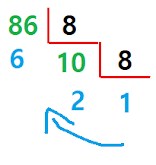
Para convertir un número decimal a octal, se utiliza un procedimiento similar al que se uso anteriormente. La diferencia es que esta vez, en lugar de dividir por 2, vamos a dividir por 8. Realizando este procedimiento, obtenemos que el equivalente al numero 86 en base 8 es: 126₈

DE DECIMAL A HEXADECIMAL

Nuevamente, utilizamos el mismo metodo que utilizamos antes, solo que esta vez vamos a dividir por 16 en lugar de 8 o 2. También hay que tener en cuenta que en los numeros hexadecimales se utilizan las letras de la A a la F para representar los digitos que no existen en el sistema de numeración decimal. Utilizando este procedimiento, obtenemos que el equivalente al numero 86 en base 16 es:   56₁₆

 OPERACIONES

86₁₀  = 1010110₂ 

 10₁₀  = 1010₂   

Suma

Para sumar dos números binarios podemos utilizar el mismo algoritmo que utilizamos para sumar números decimales, teniendo en cuenta las siguientes reglas.

Siguiendo este procedimiento, obtenemos que la suma de los números 1010110_2  y 1010₂   es igual a:

1100000₂    

Resta

Para restar dos números binarios podemos utilizar el mismo algoritmo que utilizamos para sumar números decimales, teniendo en cuenta las siguientes reglas. 

Siguiendo este procedimiento, obtenemos que la resta de los números 1010110_2  y 1010₂   es igual a: 1001100₂

Multiplicación

Para sumar dos números binarios podemos utilizar el mismo algoritmo que utilizamos para sumar números decimales, teniendo en cuenta las reglas de la multiplicación y la suma binaria

Siguiendo este procedimiento, obtenemos que la multiplicación de los números 1010110_2  y 1010₂   es igual a: 1101011100₂  

División

Para dividir dos números binarios se puede utilizar el mismo algoritmo que se utiliza para dividir números decimales. 

Se intenta dividir el dividendo por el divisor, empezando por tomar en ambos el mismo número de cifras (100 entre 110, en el ejemplo). Si no puede dividirse, se intenta la división tomando un dígito más (1001 entre 100).

Si la división es posible, entonces, el divisor sólo podrá estar contenido una vez en el dividendo, es decir, la primera cifra del cociente es un UNO. En ese caso, el resultado de multiplicar el divisor por 1 es el propio divisor. Restamos las cifras del dividendo del divisor y bajamos la cifra siguiente. Si el dividendo sigue siendo mayor al divisor luego de bajar la cifra, se pone 0 en el cociente y se baja la siguiente.

.El procedimiento de división continúa del mismo modo que en el sistema decimal.

Siguiendo este procedimiento, obtenemos que la division de los números 1010110_2  y 1010₂   es igual a: 1000₂  

---

Santiago Enriquez

CONVERSIONES

Cedula #1004 235 257

257 hexadecimal a binario

1.Hay que dividir el número entre 2 las veces posibles

257/2                                                2.Se toman los residuos de derecha a izquierda.

    1  128/2

            0  64/2

                0   32/2                             3.257 en hexa=100000001 binario

                    0   16/2

                        0   8/2

                            0   4/2

                                0   2/2

                                    0   1

100000001 binario a octal

1.Se toman grupos de 3

    100 000 001                                 Equivalencia    000    001    010    011    100    101    110    111

       4    0    1                                    Octal                    0        1        2        3        4        5        6        7

100000001 en binario= 401 en octal

100000001 en binario a hexadecimal

1Dividir el número binario en grupos de 4 de derecha a izquierda y si faltan números agregar los 0 necesarios

    0001 0000 0001                          Equivalencia 0000 0001 0010 0011 0100 0101 0110 0111 1000 

        1       0      1                                                        0     1        2        3      4       5       6       7       8

                                                        Hexadecimal  1001 1010 1011 1100 1110 1101 1111

                                                                                    9       A      B       C     D       E     F

    100000001 en binario=101 en hexadecimal

 OPERACIONES

    

---

Alejandro Rosero

CONVERSIONES

• Numero de cedula 086.774.122; Tomar los dos últimos dígitos de nuestra cedula y convertir en Hexadecimal, Octal, y Binario. En este caso 122

 

CONVERSION DE DECIMAL A BINARIO

Para realizar la conversión de cualquier cifra a binario, hay que dividir el numero del sistema decimal entre 2. El resultado se sigue dividiendo entre dos, hasta que el numero a dividir sea 1. Una vez se llega a este punto, hay que ordenar los residuos del último al primero. Este será el numero binario que buscamos del ultimo al primero. Este será el número binario que buscamos.

122 2                            

0     61 2

          1   30 2

                0    15 2

                        1    7   2

                               1    3   2

                                     1     1

122 (10) = 11110101(2)

CONVERSION DE DECIMAL A OCTAL

Para realizar la conversión de cualquier cifra a octal, hay que dividir el numero del sistema decimal entre 2. El resultado se sigue dividiendo entre ocho, hasta que el numero a dividir sea 1. Una vez se llega a ese punto, hay que ordenar los residuos del ultimo al primero. Este será el numero Octal.

122   8

2        15   8

           7     1

122(10) = 172(8)

CONVERSION DE DECIMAL A HEXADECIMAL Para realizar la conversión de cualquier cifra a hexadecimal, hay que dividir el número del sistema decimal 16, esto quiero decir que existen 16 objetos los cuales son: 0,1,2,3,4,5,6,7,8,9; A10, B11, C12, D13, E14, F,15.

122 16

  10   7                  122(10) =7a (16)

OPERACIONES

 

• Tomar los dos primeros números y los dos últimos de la cedula y hacer la conversión de Binario y se van a sumar, restar, multiplicación y división; dar una breve explicación de cada una de las operaciones.

10(10) = 1010(8)                                                                    22(10) = 10110

10 |  2                                                              22 |  2 

0      5 |  2                                                          0    11  | 2

        1      2 |  2                                                          1      5  |  2

                 0    1                                                                  1     2  |  2

                                                                                                    0    1

SUMA DE BINARIOS

Para la suma de números binarios debemos tener en cuenta los siguientes criterios:

0+0=0                            1010+

0+1=1                          10110

1+0=1                          10000

1+1=0 y llevamos 1            

RESTA DE BINARIOS

Para la resta de números binarios debemos tener en cuenta los siguientes criterios:

0-0=0                                                     10110 -

0-1=11 se pide prestado un 1                  1010

1-0=1                                                       1100

1-1=0

MULTIPLICACION DE BINARIOS

Se multiplica números de derecha a izquierda y multiplica cada dígito de un número por cada dígito del otro número, los suma. Las 3 reglas básicas de multiplicación binaria también son similares al decimal.

0*0=0                                                 

0*1=0                                          

1*0=0                                            

1*1=1

El resultado de la multiplicación de los números binarios es: 1101110

DIVISION DE BINARIOS

La División de los números binarios se realiza de manera similar al de los números decimales, siguiendo el criterio de que se debe dividir el numero mayor dividido por el menor.

El resultado de la división de binarios es 10, se hace una división normal en este caso colocamos el 1 en el cociente para mas luego multiplicarlo por el divisor en este caso el numero 1010, al realizar la multiplicación da como resultado 1010 el cual lo restamos a 1011 dando como resultado 0001 luego bajamos el siguiente numero este caso el 0 para tener el numero 00010 que al dividirlo por el divisor en este caso 1010, no alcanza entonces colocamos un 0 (cero) al cociente y obtenemos como resultado el 10.

---

Maryli Botina

CONVERSIONES

DE DECIMAL A BINARIO:

DE DECIMAL A OCTAL:

DE DECIMAL A HEXADECIMAL:

OPERACIONES

Primer paso : convertir los dos primeros y últimos dígitos de la cédula en binarios

2 primeros dígitos

SUMA

PASOS:

- Se debe tener en cuenta esta regla: 0+0=0    0+1=1   1+0= 1   1+1=0 (y llevamos 1)

- Empezamos a sumar desde la derecha, en nuestro caso:

·               0 + 0 ponemos como resultado 0, continuamos con 1+1 en el cual ponemos 0 y llevamos 1 por lo que sigue 1+0+0 que da como resultado 1, continuamos como 1+0 que da 1 y por último bajamos el 1. Obteniendo como resultado final 11100

RESTA      

PASOS: 

- Se debe tener en cuenta esta regla: 0-0=0   1-0= 1   1-1=0    0-1= no alcanza o se pide prestado al próximo

- Empezamos a restar desde la derecha, en este caso:

·         0 – 0 da como resultado 0, continuamos con 1-1 ponemos 0, seguimos con 0 – 0 da 0 y ahora en el caso de 0-1 colocamos 1 en el resultado y le sumamos 1 a la columna izquierda del sustraendo, por último, restamos 1-1 que da 0 y así obtenemos 01000               

MULTIPLICACION:

PASOS:  

- Se debe tener en cuenta estas reglas: 1*1=1    1*0=0*1=0     0*0=0   

- Se realiza de derecha a izquierda multiplicando cada digito de un número por cada dígito del otro, así:

·         Iniciamos con 0*10010 nos da 00000, seguimos con 1*10010 da 10010, 0*10010 da 00000 y por último 1*10010 es igual a 10010. Finalmente, realizamos la suma de los anteriores resultados y nos da 1 0 1 1 0 1 0 0

DIVISION:

PASOS:

-Iniciamos tomando la misma cantidad de cifras en el dividendo y en el divisor, pero en este caso como no puede dividirse se toma una cifra más en el dividendo.

- Si la división es posible colocamos 1 en el cociente ya que el divisor solo está contenido una vez en el dividendo 10010/1010=1. En el cociente restamos las cifras del dividendo con las del divisor y ese va a ser nuestro residuo, en este caso 1000. En caso de que haya más cifras continuamos bajando la siguiente.